|
| HOME |
| BLOG/NEWS |
| BIO |
| PUBLICATIONS |
| arXiv Papers |
| G-Scholar Profile |
| SOFTWARE |
| CBLL |
| RESEARCH |
| TEACHING |
| WHAT's NEW |
| DjVu |
| LENET |
| MNIST OCR DATA |
| NORB DATASET |
| MUSIC |
| PHOTOS |
| HOBBIES |
| FUN STUFF |
| LINKS |
| CILVR |
| CDS |
| CS Dept |
| Courant |
| NYU |
| Websites that I maintain |
 |
 |
 |
 |
 |
 |
Current Projects
| For a list of current projects, please visit the web site of the Computational and and Biological Learning Lab (my lab at NYU). |  |
PhD
 During my PhD, in 1985, I proposed and
published (in French), an early version of the learning algorithm known
as error backpropagation
[LeCun, 1985]
[LeCun, 1986].
Although a special form of my algorithm was equivalent to backpropagation
it was based on backpropagating "virtual target values" for the hidden
units rather than gradients. I had actually proposed the algorithm during
my Diplome d'Etudes Approfondies work in 1983/1984 but had no
theoretical justification for it back then.
The final form of the backpropagation algorithm has had a profound impact on
the fields of Machine Learning, and was the primary cause for the surge
of interest in Neural Networks in the mid 80's. Subsequently, I refined the
backpropagation algorithm, and proposed a consistent theoretical framework
for its analysis. I applied backpropagation to handwriting recognition,
medical diagnosis of abdominal pains, and intron/exon splicing site
detection in DNA sequences
[LeCun, 1987].
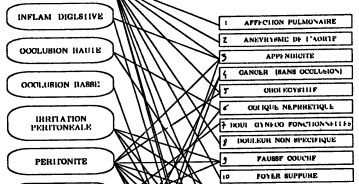
For the medical diagnosis application, I designed a network with
specific groups of hidden units to represent "syndromes". Connections
were established from symptoms (inputs) to syndroms, and from
syndromes to diagnoses (outputs) if there was a known causal relationship
between them (an early form of graphical models with logistic nodes, I guess).
I also applied multilayer nets to associative data retrieval
[LeCun and Fogelman-Soulie, 1987]
[Gallinari et al., 1987]
[Fogelman-Soulié et al., 1987c]
[Fogelman-Soulié et al., 1987b]
[Fogelman-Soulié
et al., 1987a]
During my PhD, in 1985, I proposed and
published (in French), an early version of the learning algorithm known
as error backpropagation
[LeCun, 1985]
[LeCun, 1986].
Although a special form of my algorithm was equivalent to backpropagation
it was based on backpropagating "virtual target values" for the hidden
units rather than gradients. I had actually proposed the algorithm during
my Diplome d'Etudes Approfondies work in 1983/1984 but had no
theoretical justification for it back then.
The final form of the backpropagation algorithm has had a profound impact on
the fields of Machine Learning, and was the primary cause for the surge
of interest in Neural Networks in the mid 80's. Subsequently, I refined the
backpropagation algorithm, and proposed a consistent theoretical framework
for its analysis. I applied backpropagation to handwriting recognition,
medical diagnosis of abdominal pains, and intron/exon splicing site
detection in DNA sequences
[LeCun, 1987].
For the medical diagnosis application, I designed a network with
specific groups of hidden units to represent "syndromes". Connections
were established from symptoms (inputs) to syndroms, and from
syndromes to diagnoses (outputs) if there was a known causal relationship
between them (an early form of graphical models with logistic nodes, I guess).
I also applied multilayer nets to associative data retrieval
[LeCun and Fogelman-Soulie, 1987]
[Gallinari et al., 1987]
[Fogelman-Soulié et al., 1987c]
[Fogelman-Soulié et al., 1987b]
[Fogelman-Soulié
et al., 1987a]
 At the end of my PhD, my friend
Leon Bottou and I
started writing a software system called SN to experiment with machine
learning and neural networks. It was built around a home-grown Lisp
interpreter that eventually morphed into the
Lush language.
I completed this software while I was a Research
Associate in Geoff Hinton's group at the University of Toronto.
[LeCun and Bottou, 1988]
[Bottou and LeCun, 1988]
and has been using its various embodiments ever since.
At the end of my PhD, my friend
Leon Bottou and I
started writing a software system called SN to experiment with machine
learning and neural networks. It was built around a home-grown Lisp
interpreter that eventually morphed into the
Lush language.
I completed this software while I was a Research
Associate in Geoff Hinton's group at the University of Toronto.
[LeCun and Bottou, 1988]
[Bottou and LeCun, 1988]
and has been using its various embodiments ever since.
Learning Theory, Learning Algorithms
During my PostDoc in Toronto, I extended and published my thesis work on the theoretical foundation of backpropagation, and showed that back-propagation and several of its generalizations could be derived rigorously using Lagrange functions [LeCun, 1988], reprinted in [LeCun, 1992].I also briefly worked on a new "perturbative" learning algorithm called GEMINI [LeCun, Gallant, and Hinton, 1989e].
With various colleagues, I published a theoretical analysis of learning curves [Solla, LeCun, 1991]; proposed a precursor of a now common Bayesian methods for producing class probability estimates from the output of a neural network [Denker, LeCun 1991]; and experimented with a practical boosting method for training and combining the outputs of multiple pattern recognition systems [Drucker et al. 1994].
I also worked on a method for estimating the effective capacity (or effective VC-dimension) of a learning machine by fitting the training error and testing error curves [Vapnik, Levin, LeCun 1994].
One of my long-time interests is the inherently subjective nature of the notions of information, probability, complexity, and entropy (including the definitions of those used in physics). John Denker and I wrote a short paper on the subject [Denker, LeCun, 1993].
The Dynamics of (fast) Neural Net Training
 There are many hacks in the literature to accelerate the convergence
of learning algorithms for multilayer neural nets. There have been
many claims that second-order methods ought to converge faster than
plain gradient descent. Unfortunately, most second order methods found
in the classical non-linear optimization litterature are practically
useless for neural-net training because they are all designed to work
in "batch" mode (with accurate gradients and line searches). Neural
net training is known to be considerably faster with "on-line"
learning (also called stochastic gradient) where the parameters are
updated after every training sample.
There are many hacks in the literature to accelerate the convergence
of learning algorithms for multilayer neural nets. There have been
many claims that second-order methods ought to converge faster than
plain gradient descent. Unfortunately, most second order methods found
in the classical non-linear optimization litterature are practically
useless for neural-net training because they are all designed to work
in "batch" mode (with accurate gradients and line searches). Neural
net training is known to be considerably faster with "on-line"
learning (also called stochastic gradient) where the parameters are
updated after every training sample.
Therefore, during my PhD thesis, I proposed a stochastic version of the Levenberg-Marquardt algorithm with a diagonal approximation of the Hessian. The Diagonal Hessian in neural nets was shown to be very easy to compute with a "backprop" like procedure [LeCun, 1987]. Comparisons with classical non-linear optimization algorithms have been performed [Becker and LeCun, 1989].
Recent descriptions and analyses of the stochastic diagonal Levenberg-Marquardt method can be found in [LeCun et al. 1998] and [LeCun, Bottou, Orr, Muller 1998].
With Ido Kanter and Sara Solla, I published a formula for the distribution of eigenvalues of certain types of random matrices (covariance matrices of random vectors). This result was used to predict the convergence speed of adaptive filter algorithms and neural-net learning procedures [LeCun, Kanter, Solla 1991] [Kanter, LeCun, Solla 1991]. A surprising result is that Linear Least Square converges fastest when the ratio of number of samples to number of input variables is about 4.
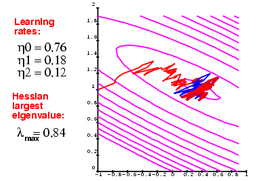
A major headache when training neural nets is how to choose the step size (learning rate) of the learning algorithm. I proposed a simple (and well justified) method for automatically computing (and adjusting) the step size for gradient-based neural-net training algorithms. It is based on a very efficient method for estimating and tracking the largest eigenvalue of the Hessian matrix of a neural nets error surface (without computing the Hessian itself) [LeCun, Simard, Pearlmutter 1993].
A recent tutorial paper on my work on efficient neural net training can be found in [LeCun, Bottou, Orr, Muller 1998].
Learning Algorithms, Generalization, and Regularization
I proposed a "pruning" (weight elimination) methods for neural networks called Optimal Brain Damage that has become quite popular over the years [LeCun, Denker, Solla, 1990].Harris Drucker and I worked on a regularization method called double backpropagation that improves the smoothness of the functions learned by multilayer neural nets (and therefore their robustness to small distortions of the inputs) [Drucker, LeCun 1992] [Drucker, LeCun 1991a] [Drucker, LeCun 1991b].
 Later, Patrice Simard and I (with J. Denker and B. Victorri) found a
regularization method called Tangent Prop that can force neural nets
to become invariant (or robust) to a set of chosen transformations of
the inputs.
[Simard, Victorri, LeCun, Denker 1992]
[Simard, LeCun, Denker, Victorri 1992].
A recent review paper on Tangent Prop (and Tangent Distance) is available
[Simard, LeCun, Denker, Victorri 1998].
Later, Patrice Simard and I (with J. Denker and B. Victorri) found a
regularization method called Tangent Prop that can force neural nets
to become invariant (or robust) to a set of chosen transformations of
the inputs.
[Simard, Victorri, LeCun, Denker 1992]
[Simard, LeCun, Denker, Victorri 1992].
A recent review paper on Tangent Prop (and Tangent Distance) is available
[Simard, LeCun, Denker, Victorri 1998].
Invariant Recognition: Convolutional Neural Networks
| Since my PhD, I had been interested in the problem of invariant visual perception, and how learning methods could help solve it. I had been experimenting with simple locally-connected neural net architectures during my PhD, and showed during my PostDoc local connections and shared weights clearly improved the performance of neural nets on simple shape recognition tasks [LeCun, 1989b] [LeCun, 1989a]. | 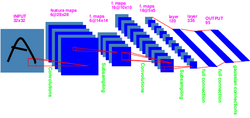 |
| Such Neural net architectures with local connections and shared weights are called Convolutional Networks. After joining AT&T Bell Labs in 1988, I applied convolutional networks to the task of recognizing handwritten characters (the initial goal was to build automatic mail-sorting machines). This work was one of the first (and one of the most cited) demonstrations that Neural Networks could be applied to "real-world" applications [LeCun et al. 1990e] [LeCun et al. 1990d] [LeCun et al. 1990a] [LeCun et al. 1989b] [LeCun et al. 1989c] [LeCun et al. 1989e]. | 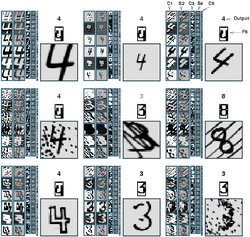 |
|
Convolutional nets are very good for recognizing individual objects
(such as characters), but they have another enormous advantage:
they can be replicated (or scanned) over large input images
extremely cheaply and act as object spotters. Replicated
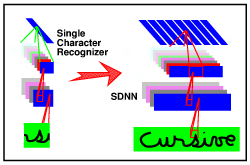
convolutional nets (also known as "Space Displacement Neural Nets")
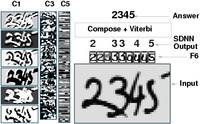
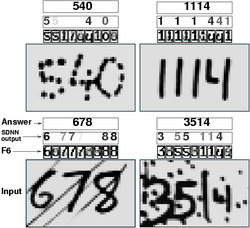
have been used to recognize digit strings (zip codes) without
requiring an explicit segmentation into characters
[Matan et al. 1992]
More experiments with SDNN are described in
[LeCun et al. 1998]
I helped design a special-purpose chip, called ANNA (With B. Boser and E. Saeckinger), that implemented this handwriting recognizer on a single piece of silicon and could recognize over 1000 characters per second (quite a feat back then) [Boser et al. 1991a] [Boser et al. 1991b] [Saeckinger et al. 1992] [Boser et al. 1992]. The chip used a mixed analog/digital scheme where the weights were stored in 4096 capacitors as analog voltages, but the inputs where digital. While convolutional nets are primarily used for object recognition and detection, they can also be used to synthesize (or generate) temporal signals such as times series (for prediction and control applications) or spatial signals. Patrice Simard and I proposed a convolutional architecture called Reverse Time-Delay Neural Net for such applications [Simard, LeCun 1992], More applications of convolutional nets are described in the following sections: face detection and pose estimation, generic object recognition in images with invariance to pose, lighting, and clutter, vision-based navigation for mobile robots, analysis and segmentation of biological images. |
|
Other Classification Algorithms: Tangent Distance, Boosting, SVM,....
Patrice Simard, John Denker and I worked on a method called Tangent Distance for measuring similarities between shapes while being robust to small distortions and displacements of the input pattern. We applied this method to handwriting recognition [Simard, LeCun, Denker 1993] [Simard, LeCun, Denker 1994]. A recent and rather complete paper on Tangent Prop and Tangent Distance is available [Simard, LeCun, Denker, Victorri 1998].
Applications: Zipcode and Check Readers
| Eventually, a development group was formed at AT&T to turn our research on handwriting recognition into operational technology [Matan et al. 1990] [Matan et al. 1992] [Burges et al. 1992] [Jackel et al. 1995]. Several products have been brought to the market, including a faxed form reader, a check reading machine (built by NCR), and an automatic teller machine that can read checks and bills deposited by bank customers (also built by NCR). A recent and detailed description is given in [LeCun et al. 1998]. | 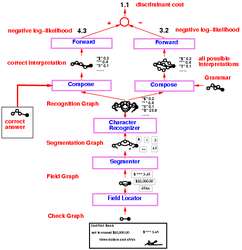 |
Applications: On-line Handwriting Recognition
 Another line of work, in collaboration with Isabelle Guyon, concerned
handwriting recognizers for pen-based computers using the idea of
"Subsampled Time-Delay Neural Network" (a special type of temporal
convolutional net) to recognize the trajectory of a stylus
[Guyon et al. 1991]
[Guyon et al. 1990]
[Guyon et al. 1992].
Another line of work, in collaboration with Isabelle Guyon, concerned
handwriting recognizers for pen-based computers using the idea of
"Subsampled Time-Delay Neural Network" (a special type of temporal
convolutional net) to recognize the trajectory of a stylus
[Guyon et al. 1991]
[Guyon et al. 1990]
[Guyon et al. 1992].
I also worked on an automatic signature verification system based on siamese networks that compute distances between objects [Bromley et al. 1994] [Bromley et al. 1993].
I briefly worked on applying similar ideas to Chinese handwriting recognition [Wu, LeCun, Jackel, Jeng 1993],
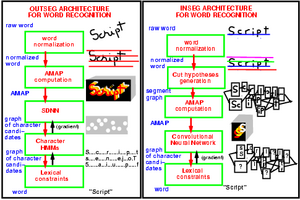
 Later, Yoshua Bengio and I started a new line of work on on-line
handwriting recognition based on "pictorial" representations
of the written words rather than on the temporal pen trajectories.
Word images enhanced with the stroke direction information were fed
to convolutional nets with great success. We also found principled
ways of combining neural nets with Hidden Markov Model. This method
allowed us to train the entire system with a discriminative
criterion at the word level.
[Bengio, LeCun, Nohl, Burges 1995]
[LeCun, Bengio 1994]
[Bengio, LeCun 1994]
[Bengio, LeCun, Henderson 1994]
A few cute applications were built around this system, including a pen-based
visitor registration system for corporate buildings
[Matic, Henderson, LeCun,
Bengio 1994].
Later, Yoshua Bengio and I started a new line of work on on-line
handwriting recognition based on "pictorial" representations
of the written words rather than on the temporal pen trajectories.
Word images enhanced with the stroke direction information were fed
to convolutional nets with great success. We also found principled
ways of combining neural nets with Hidden Markov Model. This method
allowed us to train the entire system with a discriminative
criterion at the word level.
[Bengio, LeCun, Nohl, Burges 1995]
[LeCun, Bengio 1994]
[Bengio, LeCun 1994]
[Bengio, LeCun, Henderson 1994]
A few cute applications were built around this system, including a pen-based
visitor registration system for corporate buildings
[Matic, Henderson, LeCun,
Bengio 1994].
We realized after a while that, although handwriting recognition is an interesting problem in itself, it is also a very inefficient way to communicate with a computer, except in a small number of very specific situations [Guyon, Warwick, LeCun 1996]. So we lost interest in the problem. But by working on it, we had figured out how to train a large and complex system at the word level without requiring manual segmentation. Those ideas led to the Graph Transformer Network concept and were immediately applied to recognizing bank checks.
HMM/Neural Net Hybrids, Graph Transformer Networks, Global Training of Heterogeneous Learning Machines
|
Inspired by the work of Fernando Pereira, Mehryar Mohri, Mike Riley, and
Richard Sproat on finite state transducers, Leon Bottou, Yoshua
Bengio, Patrick Haffner, and I realized that learning algorithms for
hybrid neural net/HMM systems were special cases of general
architecture in which trainable modules take valued graphs as inputs
and produce valued graphs as outputs. Such systems are called Graph
Transformer Networks [LeCun
et al. 1998] and were at the basis of the check reader system.
Similar ideas have been applied to improving the robustness of speech recognition systems using discriminative training [Rahim Bengio LeCun 1997]. | 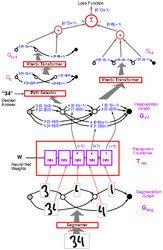 |
Document Image Compression and Digital Libraries
Between 1996 and 2001, much of my work has been centered on the DjVu project. DjVu is an image compression technology and a software platform for distributing high-resolution scanned documents over the Web.At the end of 1995, AT&T decided to spin off Lucent and NCR. Mosaic and the World Wide Web were only about 2 years old, and, as a book lover, I thought (naively) that digital libraries would become one of the Web's killer apps (naturally, just like with TV, the Web became the ultimate tool for entertainment and commerce more than for education and culture). I had just become head of Image Processing Research in the newly created AT&T Labs, and felt that our work on handwriting recognition had reached a point of diminishing return (particularly since NCR, the main outlet for our research, was spun off). So, I was looking for ways to apply our expertise in document understanding to Web-based digital libraries.
I soon realized that there was no good way of distributing high-resolution color images of scanned documents on the web. There was significant expertise in the Lab on compressing B&W textual images (with Paul Howard's work on JBIG-2), and continuous-tone images (with various work on JPEG, MPEG, and wavelets) [Cox et al. 1998] [Haskell et al. 1998]. I thought that it would be nice if we could segment the text from the pictures and backgrounds so as to compress them separately. DjVu was born.
DjVu can compress scanned documents at 300dpi in B&W to 5KB-30KB per page (3-8 times better than TIFF - Group IV), and color documents to 30KB-100KB per page (5-10 times better than JPEG) [Bottou et al. 2000] [Haffner et al. 1999] [Haffner, Bottou, Howard, LeCun 1999] [LeCun, Bottou, Haffner, Howard 1998] [Bottou et al. 1998] [Haffner et al. 1998] [Cox et al. 1998].
Our first research prototype was ready at the end of 1996, our first practical system at the end of 1997, and our first public release of free compressors and browser plug-ins in March 1998. Commercial versions appeared in early 1999. Version 3.0 of the software appeared in summer 2000 and is commercialized by LizardTech, who partnered with AT&T.
DjVu is now used by hundreds of website around the world to distribute documents (mostly scanned documents). I maintain several DjVu-related web sites including DjVuZone, Any2DjVu, Bib2Web, and DjVuLibre.
Face Detection
| During my short stay at Thomson's central research lab in 1991, I applied SDNN to the detection of human faces in images. [Vaillant Monrocq LeCun 1994] [Vaillant Monrocq LeCun 1993] Since then, several other groups have applied various types of neural nets to face detection by explicitely applying replicas of a recognizer at every position and at several scales. Oddly enough, none of them have used convolutional architectures, despite the tremendous computational advantage they provide in this case. |  |
More recently, we developed a real-time system that can detect human faces in images and simultaneously estimate their pose. This system uses convolutional networks trained with a loss function derived from the "Energy-Based Model" concept [Osadchy, Miller, and LeCun, 2004].

Object Detection and Recognition
|
My main research interest is learning and perception, particularly
visual perception.
We have developed systems capable of detecting and recognizing "generic" object categories, such as cars, airplanes, trucks, animals, or human figures, independently of the view point, the illumination, and surrounding clutter. The system uses convolutional networks, and runs in real time on a laptop [LeCun, Huang, Bottou, 2004]. |  |
Robotics
|
We are developing learning and vision techniques that will allow
mobile robots to navigate in complicated outdoors environments and
avoid obstacles.
In a preliminary experiment, we developed a small "truck" robot with two forward-pointing cameras. We drove the robot under manual control avoiding obstacles, in various environments (parks and backyards) while recording the video and the human-provided steering angle. We then trained a convolutional network to predict the steering angle of the human driver from a single pair of images from the cameras. We then let the robot drive itseld around. More details on the project are available here. This project was a "seedling" project for the LAGR program funded by the US government. In december 2004, we were selected as one of the 8 teams to participate in the full-scale LAGR program. More details on the project are available here. |
|
Energy-Based Models
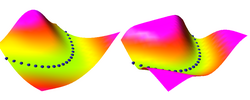 Energy-Based Models (EBMs) are a non-probabilistic form of Graphical
Model (more precisely, a un-normalized form of Factor Graph).
They associate a scalar energy to configurations of variables
that are observed and variables that must be predicted.
Energy-Based Models (EBMs) are a non-probabilistic form of Graphical
Model (more precisely, a un-normalized form of Factor Graph).
They associate a scalar energy to configurations of variables
that are observed and variables that must be predicted.
Given the values of the observed variables, the inference process in an EBM consists in finding the value of the variables to be predicted that minimizes the energy.
Learning consists in "shaping" the energy landscape so that it has minima near the desired values of the variables to be predicted. We characterize the type of loss functions that, when minimized with respect to the trainable parameters of the system, will shape the energy landscape in suitable ways [LeCun and Huang, 2005].
We demonstrate an application to face detection and pose estimation [Osadchy, Miller, and LeCun, 2004].